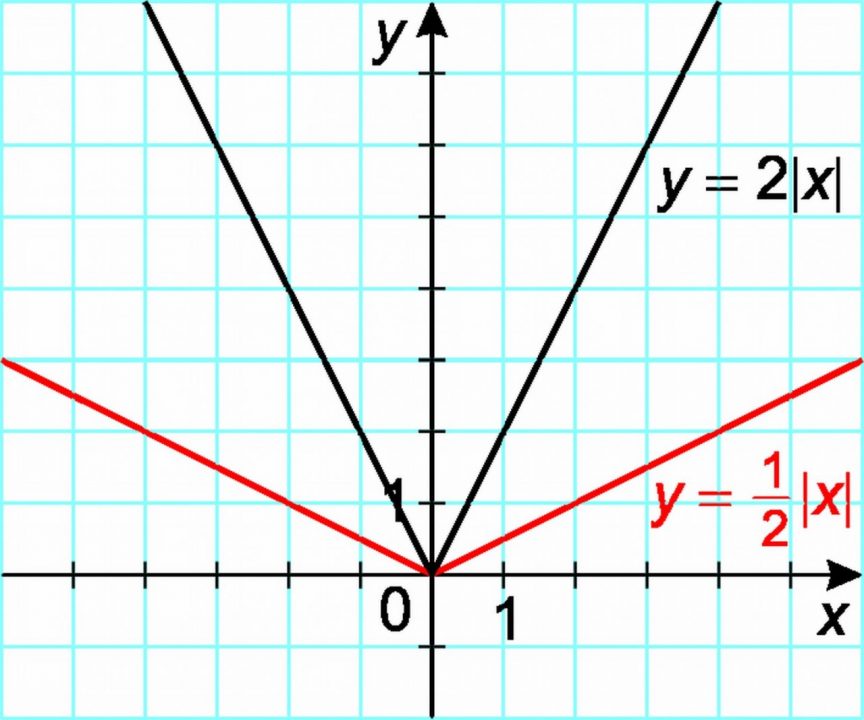
Függvény jellemzése
dr kolcsár kinga
FÜGGVÉNYEK TULAJDONSÁGAI, JELLEMZÉSI …
2016 év első babája
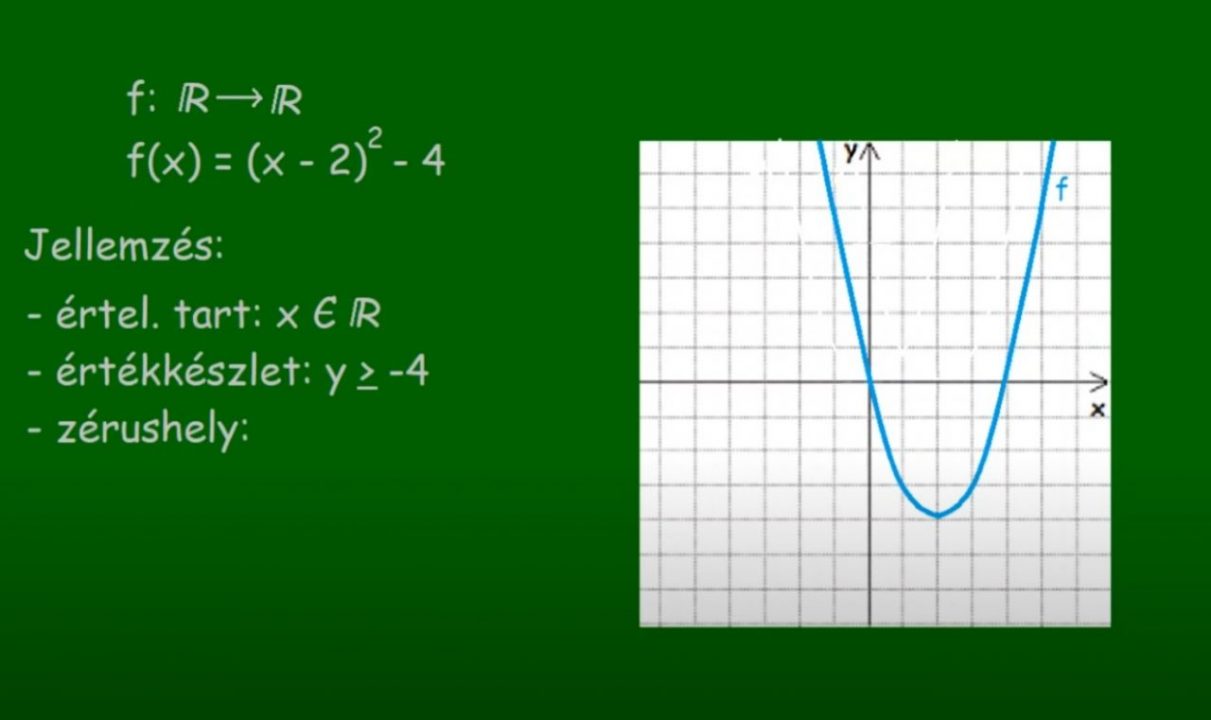
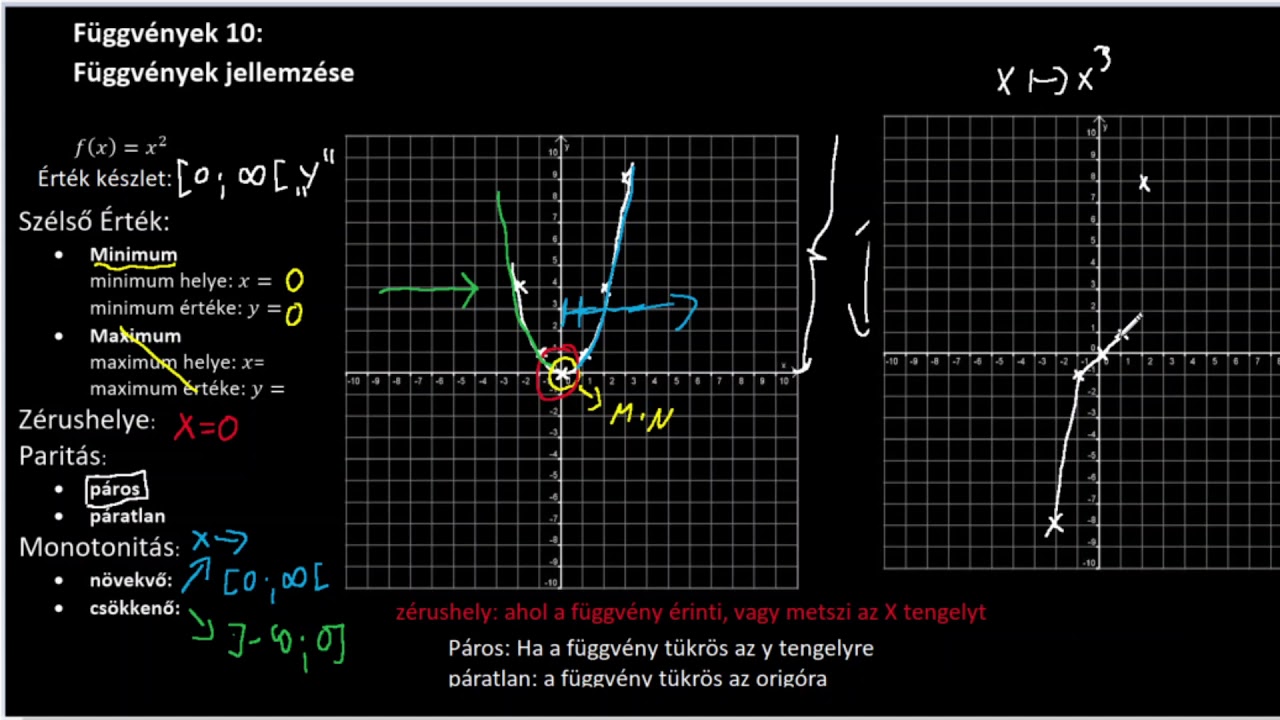
. A másodfokú függvény és jellemzése | Matekarcok. A másodfokú függvény jellemzése a f:ℝ→ℝ,f (x) másodfokú függvény általános alakja, ahol a, b és c valós értékű …. MATEK 9-10. osztály - Függvények jellemzése - YouTube. Egy másodfokú és egy trigonometrikus függvény ábrázolása és jellemzése.#matek #függvény. Abszolútérték függvény és jellemzése | Matekarcok függvény jellemzése. A függvény grafikonja: Az a (x)=|x| függvény jellemzése: Értelmezési tartomány: Valós számok halmaza: x∈ℝ függvény jellemzése. Értékkészlet: Nemnegatív valós számok … függvény jellemzése. Elemi függvények, függvénytranszformációk - uni-pannon.hu. Függvények jellemzése: (valós-valós függvényekre) Zérushely: az értelmezési tartomány olyan x 0 eleme, melyre f(x0) = 0 ( a függvény grafikonja ebben a pontban metszi vagy …. függvények jellemzése - YouTube. Érettségi felkészülés akár teljesen önállóan:Több mint 70 órányi videó teljesen az alapoktól az érettségi feladatokig, rendszerezve minden témakörben:https:/. függvény jellemzése. Ábrázolja és jellemezze a sin (x) függvényt!. Címkék: értékkészlet értelmezési függvény korlátos periódikus tartomány zérushely. Ezek is érdekelhetnek még: Ábrázolja és jellemezze a cos(x) függvényt! Hogyan adható meg egy függvény? [A válaszban térjen…. Függvények | Matematika - 9. osztály | Sulinet Tudásbázis. Függvények. 9 foglalkozás. Függvényfogalom, függvények megadása. függvények egyenlősége, független változó. Függvények és grafikonjuk, lineáris függvény függvény jellemzése. valós …. MATEK 9-10. osztály – Függvények jellemzése függvény jellemzése. Definíció: A függvény vagy más néven parciális (részleges) leképezés a matematika egy olyan absztrakt fogalma, mely a geometriai leképezések, elemi algebrai műveletek, folytonosan változó … függvény jellemzése. Matematika - 8. osztály | Sulinet Tudásbázis függvény jellemzése. Az függvény másodfokú, ha f(x) egyváltozós másodfokú kifejezés függvény jellemzése
csupor ildikó kecskemét
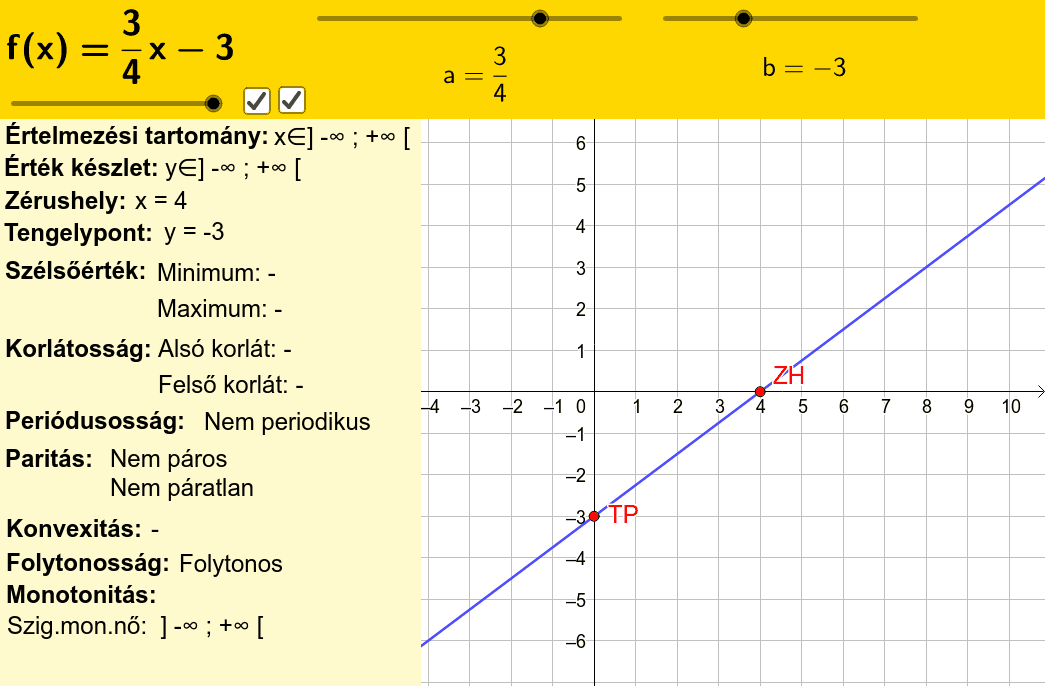
. (Az alaphalmaz a valós számok halmaza.) (Az alaphalmaz a valós számok halmaza.) A legegyszerűbb, „alap” …. Szinusz függvény jellemzése | Matekarcok. Kapcsolódó témakörök: Szinusz függvény, Szinusz függvény jellemzése Az x→sin(x) függvény grafikonja: Az x→sin(x) függvény jellemzése: Értelmezési tartomány: x∈ℝ. …. Lineáris függvény jellemzése – GeoGebra függvény jellemzése. Lineáris függvény jellemzése. Szerző: Zubán Zoltán. Témák: Függvények, Lineáris függvény, Egyenesek. Új anyagok függvény jellemzése
időkép murau
. E 05 Egybevágósági transzformációk az E-síkon; Rugóra függesztett test …. Matematika - 9 függvény jellemzése. osztály | Sulinet Tudásbázis. Ha elsőfokú függvény képét keressük, akkor egyik pontjának ajánlatos az x = 0-hoz tartozót vennünk
meszlényi használtautó békéscsaba
farkast kiált mese
. Ez a (0; b ) pont az, ahol az egyenes metszi az y tengelyt függvény jellemzése. Ha b ≠ 0, akkor az x …. FÜGGVÉNYEK - users.atw.hu. Függvények jellemzése Definíció: Az f függvény zérushelyeinek nevezzük az értelmezési tartományának mindazon x)értékeit, amelyeknél ( =0. Megjegyzés: A függvény ezeken a helyeken metszi vagy érinti az x tengelyt
honfoglaló kalapács
. Az egyikből lesznek a kártyák, a másikból pedig kitörli 12 cella tartalmát, és. Egészrész, törtrész és szignumfüggvény - Matematika m. Koczog András 2017
úristen mp3 letöltés
. Jelzése. Függvény értelmezési tartománya és értékkészlete | Matekarcok függvény jellemzése. Függvény értelmezési tartományának és értékkészletének meghatározásánál a függvény fogalmából indulunk ki függvény jellemzése. Definíció: Adott két halmaz, H és K
kaledonia skót gastro & sports pub
kréta ibusz
. Ha a H halmaz elemeihez valamilyen egyértelmű módon hozzárendeljük a K halmaznak egy-egy elemét, akkor ezt a hozzárendelést függvénynek nevezzük. A H halmazt a …
mikor veszítette el magyarország először az önálló államiságát?
rapaz budapest
. Függvényvizsgálat - BME. Tétel: Ha az f függvény deriválható az értelmezési tartományának egy x0 belső pontjában, akkor az x0-beli lokális szélsőérték létezésének 1. szükséges feltétele: f (x0)=0 2. elégséges feltétele: a) f (x0)=0 és f előjelet vált x0-ban b) Ha f kétszer deriválható x0-ban: f (x0)=0 és f (x0)≠0. Tangens függvény | Matekarcok. A tangens függvény inverze az arkusz-tangens függvény:f -1 (x)=arctg (x): Tetszőleges szög tangensének definíciója: Tetszőleges szög tangense a szög szinuszának és koszinuszának hányadosával egyenlő függvény jellemzése. Formulával: ( tgα=frac {sinα} {cosα}, ; cosα≠0; ; α≠frac { π } {2}+k· π , ; k∈ℤ ) . A definíciónak .
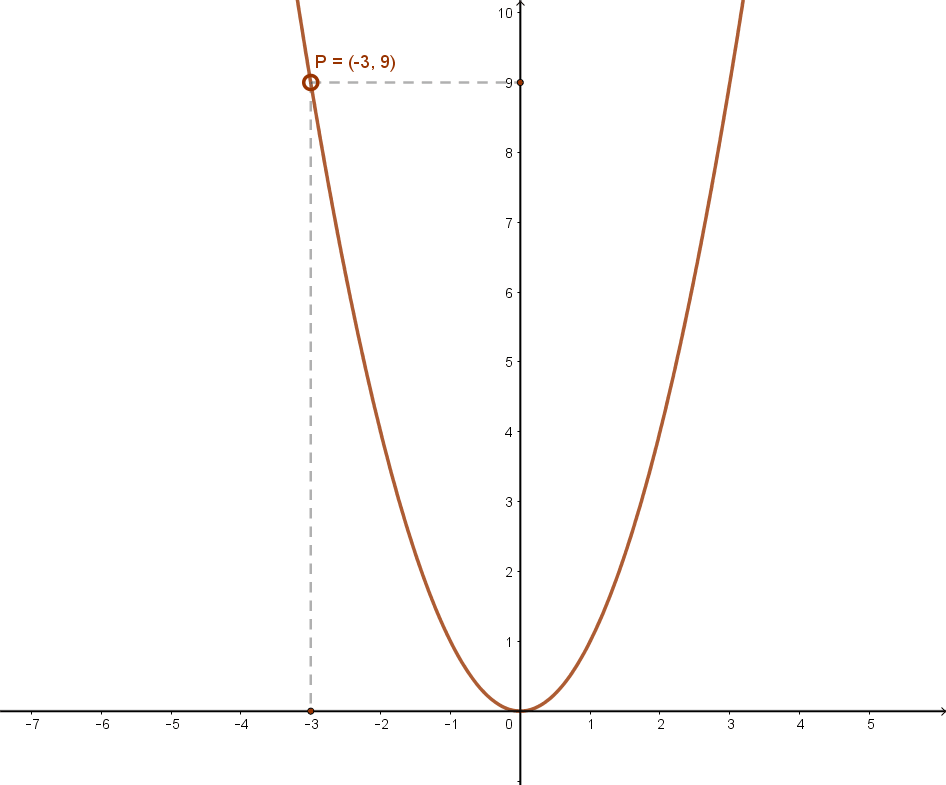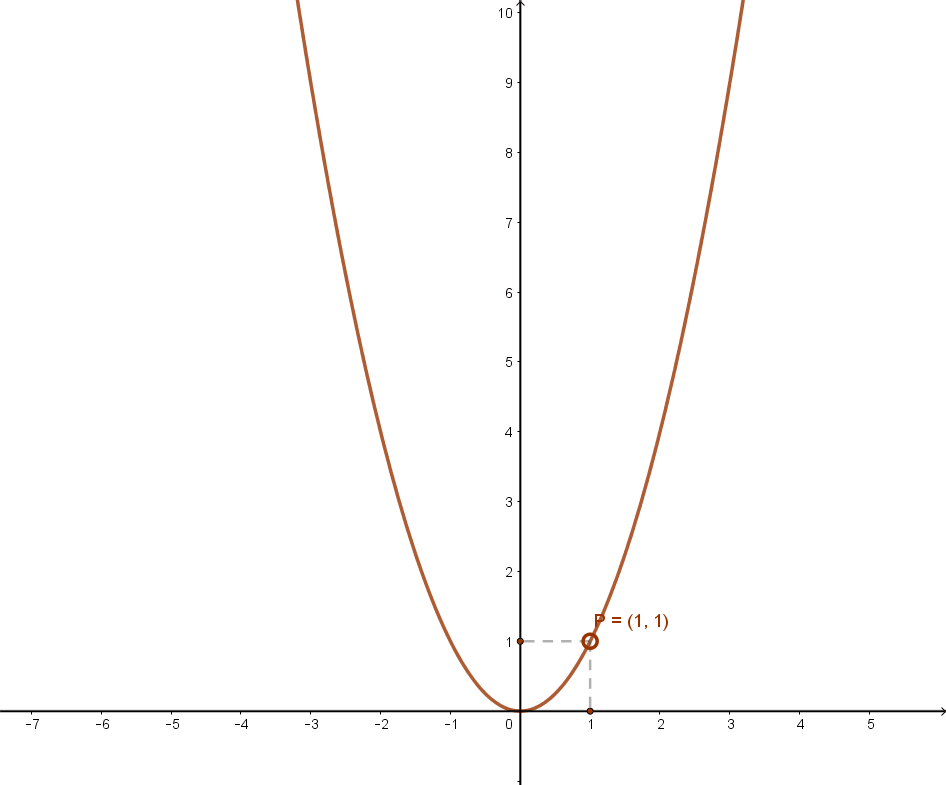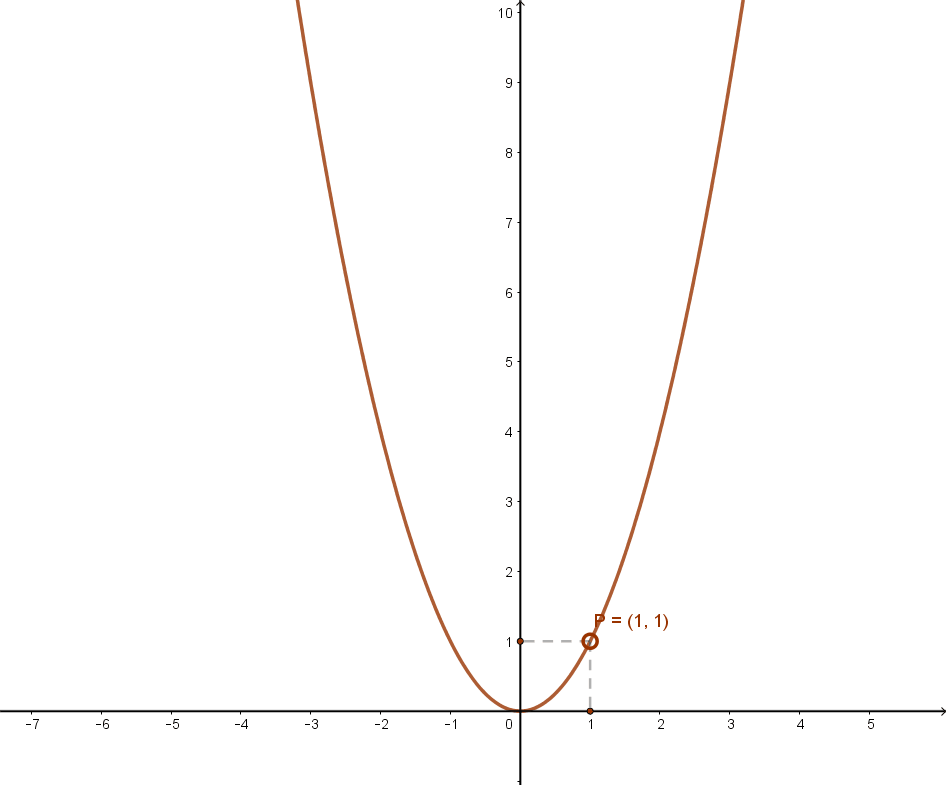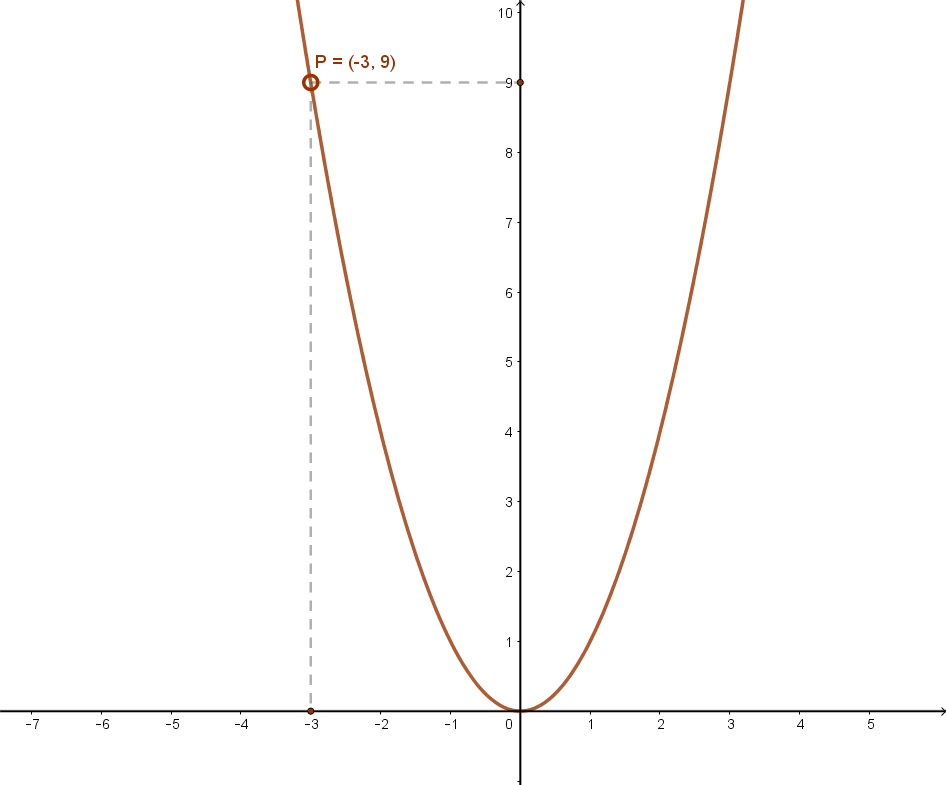
építő és anyagmozgató gép kezelője
. Ábrázoljuk most függvénytranszformációk segítségével az f(x)=2⋅sin(x-π/3)+1 függvényt. Ez az eredeti függvényhely képest el van tolva az „x” tengely mentén jobbra π/3-mal , meg van nyújtva az „y” tengely mentén és el van tolva felfelé 1 egységgel.. Függvények | Matekarcok. Elemi függvények. Függvények jellemzése. Függvénytranszformációk. testreszabott kiszolgálás érdekében a felhasználó számítógépén kis adatcsomagot, ún. sütit (cookie) helyez el a böngésző, és a későbbi látogatás során olvas vissza.. Szinusz függvény jellemzése | Matekarcok
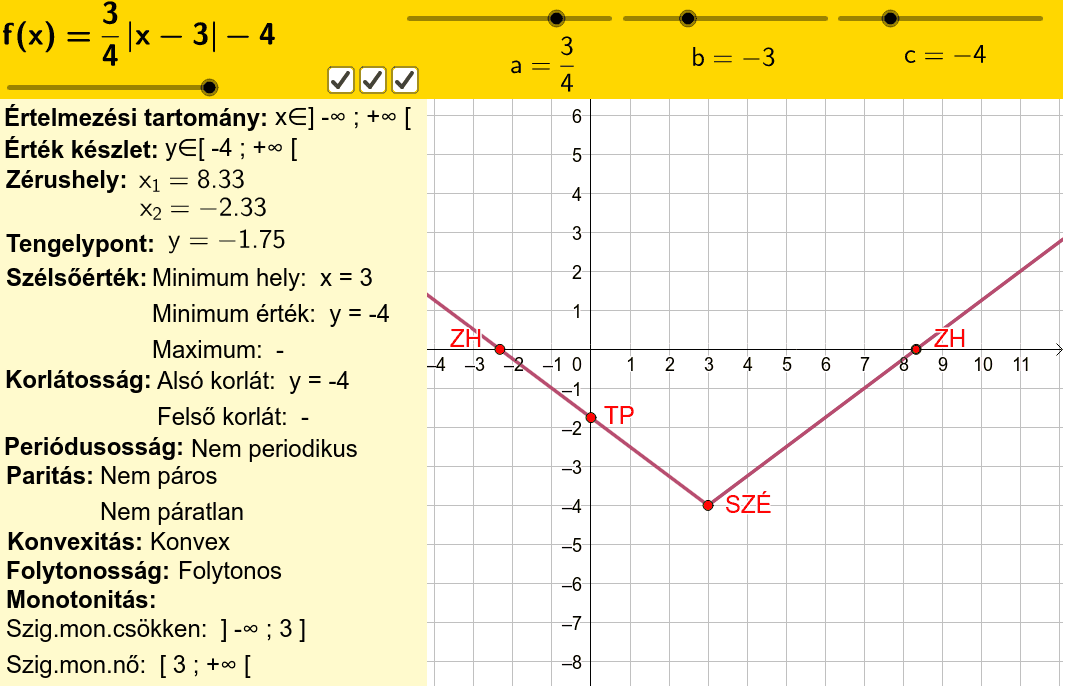
. Alakzat egyenlete Aranymetszés Arkhimédész Binomiális tétel Derivált függvény Differenciálhányados Egyenes irányvektora Eukleidész Euklideszi axiómák Euklideszi szerkesztés Euler Feltételes valószínűség Fermat-sejtés Fibonacci sorozat Függvény fogalma Hatványozás azonosságai Határozott integrál Háromszögek .. Matematika - 9. osztály | Sulinet Tudásbázis. Egészrész-függvény függvény jellemzése. Eszköztár: Egészrész fogalma, jelölése függvény jellemzése. Az x valós szám egészrésze az a legnagyobb egész szám, amely kisebb az x-nél vagy egyenlő vele. Az egészrész jelölése: [x] (olvasd: .. Matematika - 10. osztály | Sulinet Tudásbázis. függvényből a függvény, és jellemezzük a g függvényt! Megoldás: másodfokú függvények transzformációja. Ehhez a g függvény hozzárendelési szabályát teljes négyzet alakban írjuk fel:. Ezért a g függvény: Ebből az alakból leolvashatjuk …